V inženýrské praxi se často setkáváme s určitými integrály, které
není možné vyčíslit analyticky, je tedy nutné numerické vyčíslení. Jako
příklad uveďme úlohu U14.4 ze skript Chemické inženýrství I (vsádková
destilace). Za předpokladu nekonstantní relativní těkavosti benzenu vůči
toluenu je zde nutné vyčíslit integrál funkce F = 1/(u
− w), kde u a w jsou hmotnostní zlomky
benzenu v parní a kapalné fázi. Fáze jsou v rovnováze, platí tedy
u = u(w). Hodnoty w dle zadání a jim
odpovídající hodnoty u zapíšeme v Pythonu jako seznamy
liq_frac a vap_frac:
liq_frac = [0.2, 0.25, 0.3, 0.35, 0.4]
vap_frac = [0.374, 0.4455, 0.5101, 0.5687, 0.6219]Z těchto hodnot poté vypočítáme funkční hodnoty F. Nejdříve
vytvoříme prázdný seznam func. Poté do něj postupně ve
for cyklu pomocí příkazu append zapíšeme
hodnoty F. V cyklu iterujeme přes liq_frac a
vap_frac spojené do uspořádané n-tice funkcí
zip.
func = []
for liq_frac_value, vap_frac_value in zip(liq_frac, vap_frac):
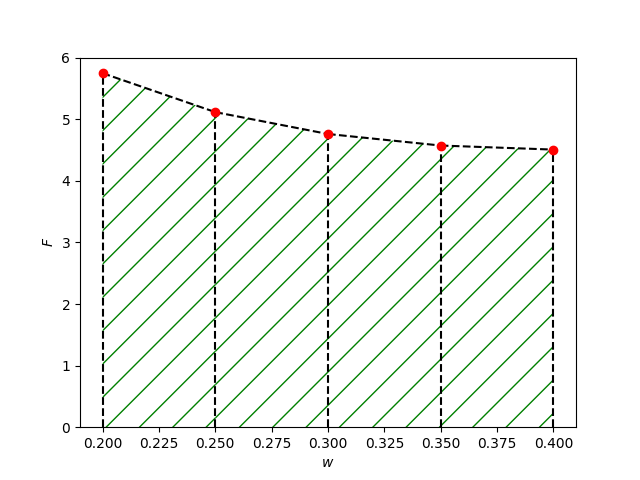
func.append(1 / (vap_frac_value - liq_frac_value))Integrál funkce F mezi zadanou horní a dolní mezí w vyčíslíme lichoběžníkovou metodou. Tato metoda aproximuje integrál součtem ploch lichoběžníků, které jsou určeny hodnotami F a w, viz obrázek.

Vlastní implementaci lichoběžníkové metody zapíšeme v Pythonu
následujícím způsobem. Nejdříve vytvoříme prázdný seznam
trapezoid. Ve for cyklu do něj pomocí příkazu
append zapíšeme plochy jednotlivých lichoběžníků. Pro
výpočet plochy lichoběžníku je nutné znát dvě po sobě následující
hodnoty w a F. Iterujeme přes liq_frac a
liq_frac[1:], tedy současná a následující hodnota
w. Analogicky pro F iterujeme přes func a
func[1:].
trapezoid = []
for liq_frac_value, func_value, next_liq_frac_value, next_func_value in zip(liq_frac, func, liq_frac[1:], func[1:]):
trapezoid.append((next_liq_frac_value - liq_frac_value) * (0.5 * (next_func_value + func_value)))Poté vypočítáme výsledný integrál jako součet ploch všech
lichoběžníků pomocí funkce sum a pomocí print
vypíšeme výsledek na obrazovku.
integral = sum(trapezoid)
print(trapezoid)