5. Numerické řešení soustav nelineárních rovnic

Soustavou nelineárních rovnic myslíme takovou soustavu rovnic, z nichž je alespoň jedna nelineární. Vzhledem k tomu, že většina nelineárních rovnic, resp. soustav nelineárních rovnic, není řešitelná analyticky, musíme jejich kořeny hledat pomocí numerických metod, např. metodou půlení intervalu nebo Newtonovou metodou. Jazyk Python má nicméně ve svých knihovnách k dispozici numerické řešiče, které je možno rychle implementovat. V této kapitole budeme potřebovat knihovnu sympy. Tu můžeme nainstalovat pomocí příkazu pip install sympy.

Numerické řešení jedné nelineární rovnice

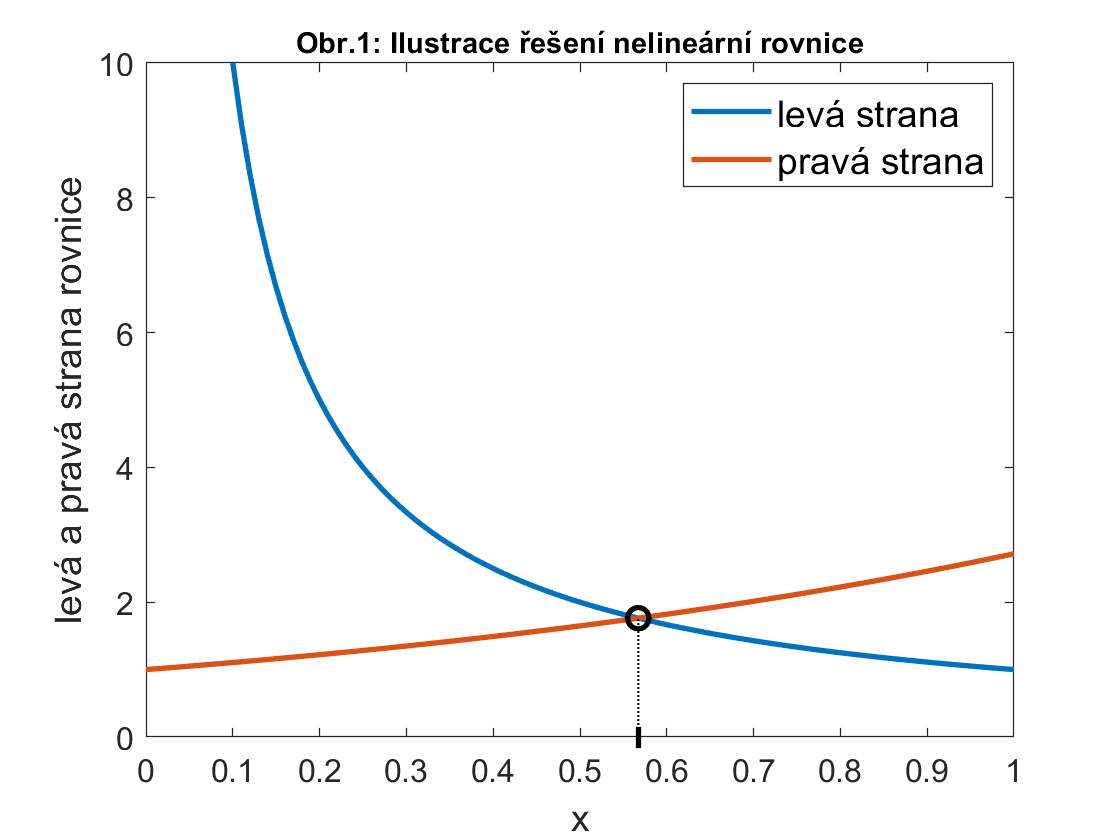
Jako příklad vezměme rovnici 1/x = exp(x), viz Obr.1. Hledáme takovou hodnotu proměnné x, jež danou rovnici splňuje.

Obr.1: Ilustrace řešení nelineární rovnice 

    from sympy import Symbol, Eq, nsolve
    
    x = Symbol("x", real=True)
    rovnice = Eq(1 / x, exp(x))
    pocatecni_nastrel = 0.5
    reseni = nsolve(rovnice, x, pocatecni_nastrel)
    print(reseni)

Při správném spuštění tohoto programu se na obrazovku vypíše řešení, přibližně 0.5671. Výsledek můžeme ještě dosadit zpět do x, pokud potřebujeme s vyčíslenou hodnotou dále pracovat.

   x = reseni

Numerické řešení soustavy dvou nelineárních rovnic

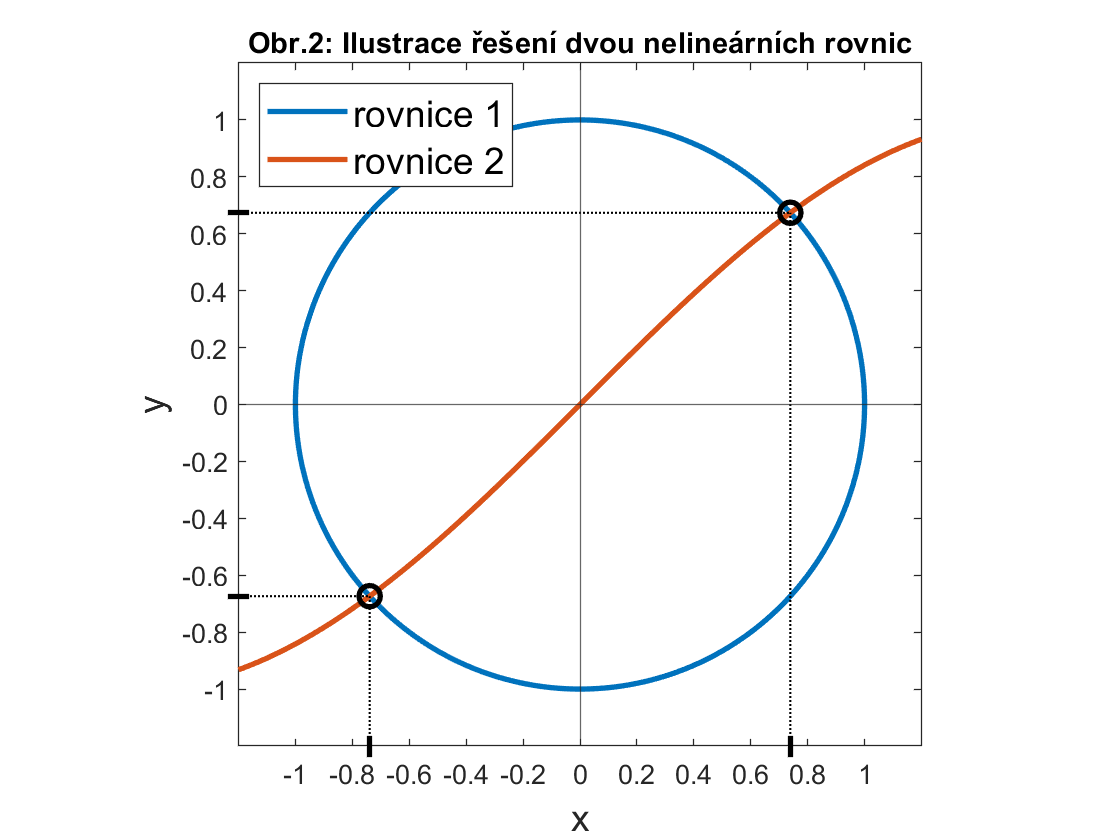
Pomocí funkce nsolve lze rovněž řešit soustavu dvou i více nelineárních rovnic. Pro příklad nalezněme průsečíky jednotkové kružnice se středem v počátku souřadnic a jednoduchou sinusoidou, zapsané rovnicemi rovnice1 a rovnice2, viz Obr.2.

Obr.2: Ilustrace řešení dvou nelineárních rovnic 

    from sympy import Symbol, Eq, nsolve
    
    x = Symbol("x", real=True)
    y = Symbol("y", real=True)
    nezname = [x, y]
    
    rovnice1 = Eq(x ** 2 + y ** 2 - 1, 0)
    rovnice2 = Eq(y - sin(x), 0)
    soustava_rovnic = [rovnice1, rovnice2]

    pocatecni_nastrel = [1, 1]

    reseni = nsolve(soustava_rovnic, nezname, pocatecni_nastrel)
    print(reseni)

Při správném spuštění tohoto programu se na obrazovku vypíše řešení, přibližně 0.7391 a 0.6736. Výsledek můžeme ještě dosadit zpět do x a y, pokud potřebujeme s vyčíslenými hodnotami dále pracovat.

   x, y = reseni

Pokud zvolíme počáteční nástřel např. [-1, -1], program nalezne druhé řešení odpovídající hodnotám -0.7391 a -0.6736.

Ilustrace na reálném příkladu

V této sekci spočteme soustavu čtyř rovnic o čtyřech neznámých, vycházejících z reálného příkladu (Úloha 15-6b v Chemickém inženýrství I, kapitola Chemické reaktory).

Poznamenejme, že v této úloze se jedná o návrhový výpočet, v němž známe parametry na vstupu i na výstupu, a máme za úkol zjistit počet reaktorů v kaskádě, abychom získali požadovanou kumulativní konverzi vstupní suroviny.

Výňatek z úlohy

Nejprve zde deklarujme mezivýsledky, které vycházejí z řešení 15-6a.

    from sympy import Symbol, Eq, nsolve

    nuA, nuB, nuC = -2, 1, 1  # stech koef
    k_plus = 5.0  # m3/kmol/h
    k_minus = 0.3125  # m3/kmol/h
    V0 = 6.2745  # m3
    cA0, cB0, cC0 = 1.50, 0.0, 0.0  # kmol/m3
    cAN, cBN, cCN = 0.433, 0.533, 0.533  # kmol/m3
    tau_dash = 0.062745  # h
    zetaAN = 0.711

Nyní proveďme řešení jedné iterace, tj. vypočteme kumulativní konverzi pro N-1 reaktor, kde N značí poslední reaktor v kaskádě. Takovéto řešení kaskády “odzadu” má výhodu v tom, že se vyhneme kvadratické rovnici (s neznámou kumulativní konverzí obecně k-1 reaktoru), jejíž výstupy bychom museli ošetřovat.

# Bilance slozky A v poslednim reaktoru (N) v kaskade
cAN_1 = cAN - nuA * (k_plus * cAN ** 2 - k_minus * cBN * cCN) * tau_dash

cAN_2 = Symbol("cAN_2", real=True)
cBN_1 = Symbol("cBN_1", real=True)
cCN_1 = Symbol("cCN_1", real=True)
zetaAN_1 = Symbol("zetaAN_1", real=True)

# Rovnice pro reaktor N-1
rce1 = Eq(cAN_2 - cAN_1 + \
    nuA * (k_plus * cAN_1 ** 2 - k_minus * cBN_1 * cCN_1) * tau_dash, 0)
rce2 = Eq(cAN_1, cA0 * (1 - zetaAN_1))
rce3 = Eq(cBN_1, cB0 - nuB / nuA * cA0 * zetaAN_1)
rce4 = Eq(cCN_1, cC0 - nuC / nuA * cA0 * zetaAN_1)
rovnice = [rce1, rce2, rce3, rce4]

nezname = [cAN_2, cBN_1, cCN_1, zetaAN_1]

pocatecni_nastrel = [cAN_1, cBN, cCN, zetaAN]
reseni = nsolve(rovnice, nezname, pocatecni_nastrel)
cAN_2, cBN_1, cCN_1, zetaAN_1 = reseni
print(zetaAN_1)

Kumulativní konverze v N-1 reaktoru by měla vyjít 0.640. Vzhledem k tomu, že je tato hodnota kladná, musíme v příkladu analogicky řešit tyto rovnice v další iteraci.