Vektory i matice jsou v balíčku NumPy reprezentovány stejnou třídou
ndarray. Jak název napovídá, jedná se o obecně
N-dimenzionální pole (v tomto kurzu si vystačíme se dvěma dimenzemi).
Instance ndarray ze sekvencí vytváříme pomocí funkce
array:
import numpy as np
v = np.array([1, 2, 3]) # vektor o 3 prvcích (1D pole)
M = np.array([[1.0, 2.0, 3.0], [4, 5, 6], [7, 8, 9]]) # matice 3x3 (2D pole)> array([1, 2, 3])
> array([[1., 2., 3.],
[4., 5., 6.],
[7., 8., 9.]])NumPy také obsahuje mnoho šikovných konstrukčních funkcí pro specifické případy, například:
zeros matice s nulovými prvkyones matice s jedničkovými prvkyeye jednotková maticediag diagonální maticelinspace, logspace vektor s lineárním,
resp. logaritmickým rozložením prvkůarange vektor s pravidelným rozložením prvkůOproti vnořeným seznamům mají vektory a matice v NumPy několik specifik:
M.shape # tvar matice
M.dtype # datový typ prvků> (3, 3)
> dtype('float64')Indexování a slicing má podobnou syntaxi jako např. v jazyku MATLAB,
je třeba si dát pozor, že python indexuje od nuly. Pro 2D pole se
používá dvojice indexů [řádek, sloupec]:
M[0, 1] # prvek na řádku 1, sloupci 2
M[1, :] # druhý řádek
M[:, 1] # druhý sloupec
M[1] # druhý řádek (zkrácený zápis broadcastingu)
M[:2, :2] # první dva řádky a sloupce> 2.0
> array([4., 5., 6.])
> array([2., 5., 8.])
> array([4., 5., 6.])
> array([[1., 2.],
[4., 5.]])NumPy obsahuje mnoho funkcí pro práci s maticemi, např. transpozice, inverze, determinant, vlastní čísla, SVD. V tomto textu se zaměříme na řešení soustav lineárních rovnic, pro další funkce se podívejte do dokumentace. Nutno podotknout, že vedle balíčku NumPy existuje i jakási “nadstavba” SciPy, která obsahuje mnoho pokročilých funkcí pro numerické výpočty v Pythonu.
Mějme soustavu lineárních rovnic ve tvaru Ax = b, kde
A je matice soustavy, x je vektor neznámých a
b je vektor pravých stran. V NumPy se řešení soustavy
provádí funkcí solve z modulu
numpy.linalg:
A = np.array([[1.0, 2.0], [-2.0, 3.0]])
b = np.array([14.0, 7.0])
x = np.linalg.solve(A, b)> array([5., 2.])Kontolu správnosti provedeme vynásobením matice A
výsledným vektorem x a porovnáním s vektorem pravých stran
b, to lze provést následujícím způsobem:
A @ x
np.matmul(A, x) # alternativní zápis> array([14., 7.])Při rektifikaci směsi fenolů obsahujících molárně 35 % fenolu, 40 % kresolu, 20 % xylenolu a 5 % těžších fenolů se získává destilát o molárním složení 95 % fenolu a 5 % kresolu. Destilát obsahuje 90 % z celkového látkového množství fenolu z nástřiku. Zjistěte látkové množství destilátu a zbytku vzhledem k nástřiku 100 kmol. Vypočtěte rovněž složení zbytku v molárních %.
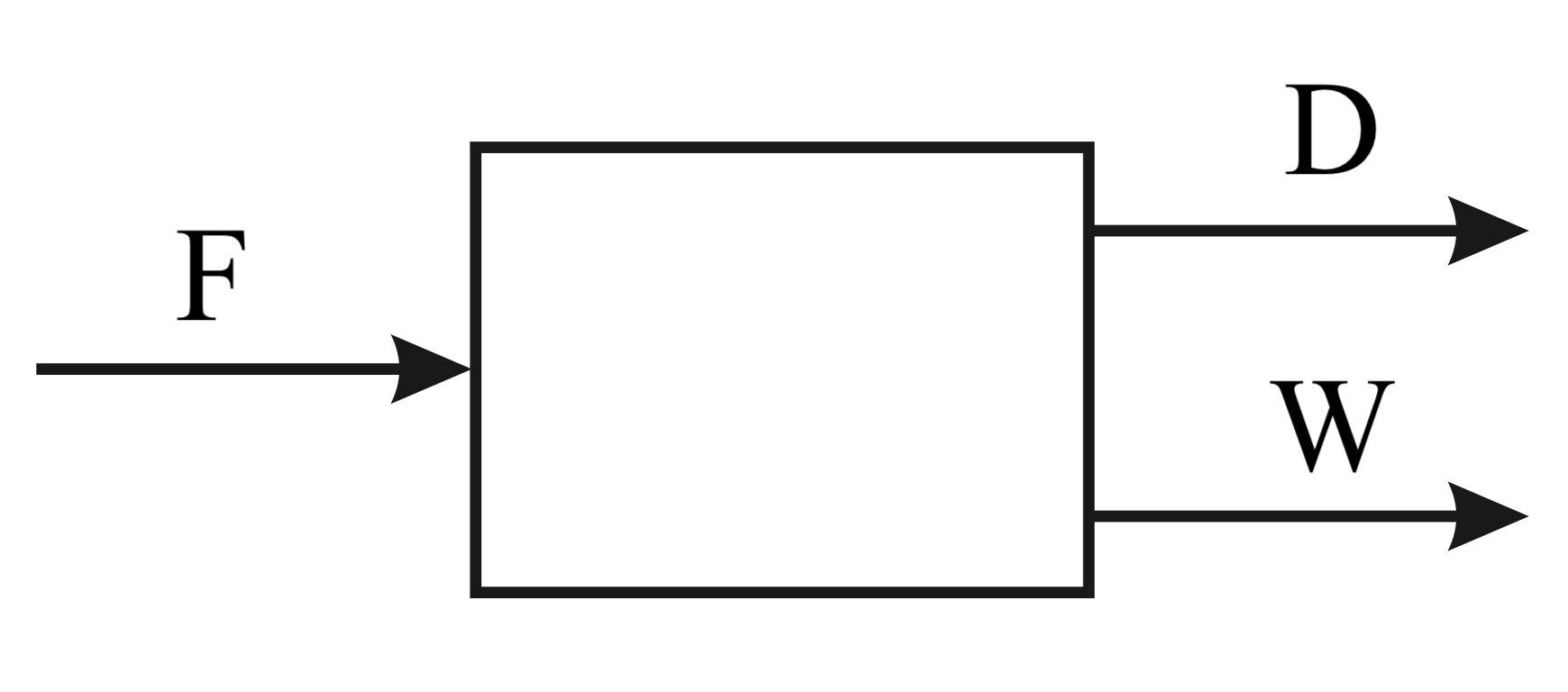
Naším úkolem je provést bilanci látkového množství pro systém s
jednou jednotkovou operací (rektifikace), která má jeden vstupní proud
(nástřik zn. F) a dva výstupní proudy (destilát
D a zbytek W). Náš systém obsahuje formálně 4
složky: (A) fenol, (B) kresol,
(C) xylenol a (D) těžší fenoly. Je zadáno
složení nástřiku a destilátu v molárních procentech, dále je zadáno
celkové látkové množství nástřiku (základ výpočtu) a informace o obsahu
fenolu v destilátu (dodatkový vztah). Cílem výpočtu je dopočítat látkové
množství destilátu a zbytku, dále je nutné určit složení zbytku v
molárních procentech.

Náš systém má 6 neznámých: celkové látkové množství destilátu
nD, celkové látkové množství zbytku nW a
molrární zlomky v destilačním zbytku xAW, xBW,
xCW a xDW.
xAF, xBF, xCF, xDF = 0.35, 0.40, 0.20, 0.05
xAD, xBD, xCD, xDD = 0.95, 0.05, 0.00, 0.00
nF = 100.0 # kmolvšiměte si, že Python umožňuje přiřadit více proměnných najednou v jednom příkazu, jedná se o tzv. multiple assignment.
Aby bylo řešení bilance jednoznačně určeno, musíme sestavit 6 rovnic. Využijeme 4 bilance látkového množství pro každou ze složek, dále dodatečnou podmínku na obsah fenolu v destilátu a vaznou podmínku pro molární zlomky v destilačním zbytku (jejich suma se musí rovnat 1).
Tímto způsobem ale dojdeme k systému tzv. bilineárních rovnic, což je
v těchto typech příkladů velmi časté. Zjednodušením je zavedení
substituce na bilieární členy xiW * nW = niW. Místo
počítání s molárními zlomky budeme počítat přímo s látkovým množstvím
jednotlivých složek, podmínka na sumu zlomků se tedy promění na celkovou
látkovou bilanci.
Pomocí balíčku NumPy si definujeme matici soustavy A a vektor pravých
stran b, arbitrárně jsme si zvolili pořadí proměnných ve vektoru
neznámých takto: x = [nD, nW, xAW, xBW, xCW, xDW].
import numpy as np
A = np.array([[xAD, 0, 1, 0, 0, 0],
[xBD, 0, 0, 1, 0, 0],
[xCD, 0, 0, 0, 1, 0],
[xDD, 0, 0, 0, 0, 1],
[xAD, 0, 0, 0, 0, 0],
[0, -1, 1, 1, 1, 1]])
b = np.array([xAF * nF,
xBF * nF,
xCF * nF,
xDF * nF,
0.9 * xAF * nF,
0])všiměte si, že Python dovoluje rozdělovat dlouhé řádky uvnitř závorek bez použití
\, toto je nazýváno implicitní spojování řádků
Soustavu vyřešíme funkcí solve z modulu
numpy.linalg.
x = np.linalg.solve(A, b)
nD, nW, nAW, nBW, nCW, nDW = xNyní jen zbývá dopočítat molární zlomky v destilačním zbytku.
xAW = nAW / nW
xBW = nBW / nW
xCW = nCW / nW
xDW = nDW / nWZobrazíme výsledky v poždaovaném formátu, využijeme tzv.
f-string pro formátování výstupu. Je to jeden z nejčitelnějších
způsobů formátování řetězců v Pythonu. Výrazy jsou ohraničeny složenými
závorkami {} a mohou obsahovat specifikátory formátu. Pro
formátování desetinných čísel platí
{<hodnota>:<šířka pole>.<počet zobrazených desetinných míst>f}.
print(f"Destilát: {nD:.1f} kmol")
print(f"Zbytek: {nW:.1f} kmol")
print(f"Složení zbytku: {xAW * 100:.1f} % fenol, {xBW * 100:.1f} % kresol, {xCW * 100:.1f} % xylenol, {xDW :.1f%} % těžší fenoly")Výstupem je:
> Destilát: 33.2 kmol
> Zbytek: 66.8 kmol
> Složení zbytku: 5.2 % fenol, 57.4 % kresol, 29.9 % xylenol, 7.5 % těžší fenoly