Jak už název napovídá, balíček SymPy se používá pro symbolické zobrazení, úpravy a řešení rovnic. Tedy více odpovídá postupu, kterým bychom postupovali, kdybychom úlohu řešili ručně na papíře. Balíček SymPy nahrajeme stejně, jak jsme již zvyklí. Balíček můžeme načíst pod jakýmkoliv názvem, nicméně zde se budeme řídit konvencemi.
import sympy as smKlasicky jsme v Pythonu zvyklí, že než nějakou proměnnou použijeme, musíme ji zadefinovat. To většinou znamenalo, že jsme museli znát její hodnotu a priori. Obvykle se jedná o hodnoty ze zadání úlohy a podobně. Takové neznámé nemůžeme explicitně využít a lze je získat pouze řešením (bilančních) rovnic či výpočtem rovnice (například při hledání tlaku nasycených par z Antoineovy rovnice).
V případě balíčku SymPy je tomu jinak, protože zde můžeme používat i
proměnné, které jsou na počátku neznámé a v rovnicích budou následně
vystupovat díky symbolické reprezentaci. I zde je ale potřeba proměnnou
na začátku nadefinovat jako symbolickou. Pokud na začátku nezadefinujeme
proměnnou x Python si s ní neporadí.
expr = x + 1> Traceback (most recent call last):
> NameError: name 'x' is not definedPokud však proměnnou definujeme pomocí příkazu
sm.symbols jako symbol, problém již nenastane.
x = sm.symbols('x')
expr = x + 1
print(expr)> x + 1Pro vyčíslení funkce nebo výrazu pro nějakou hodnotu proměnné
x, stačí použít příkaz subs. Tento příkaz
nahradí symbolickou proměnnou zadanou hodnotou. Důležité je, že původní
výraz expr zůstává nezměněný - subs totiž
vytváří nový upravený výraz.
exprVal = expr.subs(x, 2)
print(exprVal)
print(expr)> 3
> x + 1Jedním ze zajímavých využití balíčku SymPy může být definice
libovolné funkce přímo symbolicky a její následná derivace podle námi
zvolené proměnné. Představme si, že máme následující rovnici popisující
enthalpickou bilanci pro ideálně míchaný průtočný reaktor s exotermní
reakcí 1. řádu a s recyklem (model CSTR1EXO), u které nás zajímá její
první derivace (řekněme podle proměnné theta). Jednou z
možností je použít numerickou derivaci pomocí vícebodové aproximace.
Alternativně lze využít balíček SymPy a získat analytickou derivaci,
kterou je pak možné vyčíslit pouze v bodě, kde nás samotná derivace
zajímá.
a, theta, theta_c, da, b, beta, x, gamma = sm.symbols('a theta theta_c da b beta x gamma')
funkce_t = -a*theta + da*b*(1 - x)*sm.exp(theta/(1 + theta/gamma)) - beta*(theta - theta_c)
print(funkce_t)
der = sm.diff(funkce_t, theta)
print(der)> b*da*(1 - x)*exp(theta/(1 + theta/gamma)) - a*theta - beta*(theta - theta_c)
> b*da*(1 - x)*(1/(1 + theta/gamma) - theta/(gamma*(1 + theta/gamma)**2))*exp(theta/(1 + theta/gamma)) - a - betaDalšími zajímavými funkcemi v balíčku SymPy jsou: -
simplify: zjednodušení výrazu nebo funkce -
equals: otestování, zda jsou dva výrazy totožné -
sympify: převod proměnné ve formátu ‘string’ na SymPy výraz
- integrate: výpočet integrálu výrazu podle zadané proměnné
- limit: výpočet limity výrazu při určité hodnotě
proměnné.
Pro více informací, návodů a příkladů využití jednotlivých funkcí vás nasměruji na dokumentaci.
Řešme nyní soustavu lineárních rovnic ve tvaru Ax = b.
Zde A je matice soustavy, x je vektor
neznámých a b je vektor pravých stran. V rámci balíčku
SymPy budeme soustavu řešit pomocí funkce linsolve. Nejprve
zapíšeme naše rovnice. Zde si všimněte možnosti dvojího zápisu. První
varianta předpokládá tvar a-b=0, zatímco druhá využívá
příkaz Eq a zapisuje rovnost ve tvaru a=b
x, y = sm.symbols('x y')
eq1_a = 5*x + 1*y - 5
eq2_a = 1*x - 1*y - 4
eq1_b = sm.Eq(5*x + 1*y, 5)
eq2_b = sm.Eq(1*x - 1*y, 4)
sol_a = sm.linsolve([eq1_a, eq2_a], (x, y))
print(sol_a)
sol_b = sm.linsolve([eq1_b, eq2_b], (x, y))
print(sol_b)> {(3/2, -5/2)}
> {(3/2, -5/2)}Řešení komplikovanější soustavy lineárních algebraických rovnic si ukážeme na následujícím příkladu. Tento příklad použijeme k řešení bilančních rovnic stejné úlohy, která byla již vyřešena v minulé kapitole pomocí matic. > Při rektifikaci směsi fenolů obsahujících molárně 35 % fenolu, 40 % kresolu, 20 % xylenolu a 5 % těžších fenolů se získává destilát o molárním složení 95 % fenolu a 5 % kresolu. Destilát obsahuje 90 % z celkového látkového množství fenolu z nástřiku. Zjistěte látkové množství destilátu a zbytku vzhledem k nástřiku 100 kmol. Vypočtěte rovněž složení zbytku v molárních %.
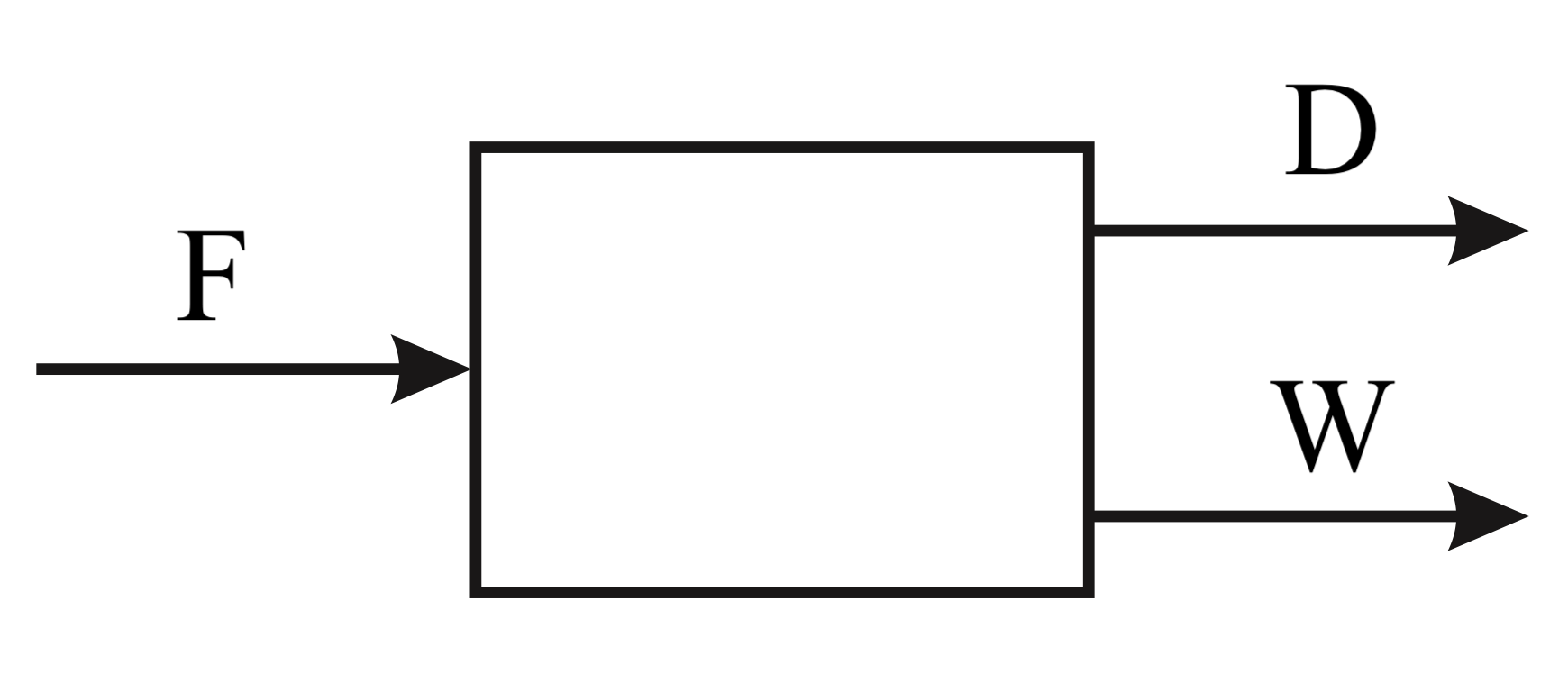
Cílem úlohy je provést bilanci látkového množství v procesu
rektifikace. Jednotková operace má jeden vstupní proud (nástřik
F) a dva výstupní proudy (destilát D a zbytek
W). V systému se nachází čtyři složky - (A)
fenol, (B) kresol, (C) xylenol a
(D) těžší fenoly. Ze zadání známe složení nástřiku a
destilátu (v mol. %), celkové množství nástřiku (v molech, základ
výpočtu) a obsah fenolu (A) v destilátu (D).
Naším úkolem je spočítat látkové množství destilátu D a
zbytku W a složení zbytku W (v mol. %).

Z bilančního schématu je zřejmé, že máme celkem tři proudy, každý s
pěti neznámými. Celkem tedy 15 neznámých. Ze zadání známe složení a
množství nástřiku (5 proměnných) a složení destilátu (4 proměnné). Zbývá
nám tedy celkem 6 neznámých, které je třeba dopočítat. Jedná se o
množství destilátu nD a zbytku nW a složení
zbytku xAW, xBW, xCW a
xDW.
import sympy as sm
xAF, xBF, xCF, xDF = .35, .40, .20, .05 # mol. %
xAD, xBD, xCD, xDD = .95, .05, .00, .00 # mol. %
nF = 100. # kmol
nD, nW, xAW, xBW, xCW, xDW = sm.symbols('nD nW xAW xBW xCW xDW')Abychom mohli úlohu jednoznačně vyřešit, je potřeba sestavit 6
nezávislých bilančních rovnic. V našem případě se bude jednat o 4
složkové bilance (f1-f4), podmínku na podíl fenolu v
destilátu (f5) a poslední podmínkou (f6) bude
o složení ve zbytku (suma zlomku se rovná 1).
f1 = sm.Eq(xAD*nD + xAW*nW, xAF*nF)
f2 = sm.Eq(xBD*nD + xBW*nW, xBF*nF)
f3 = sm.Eq(xCD*nD + xCW*nW, xCF*nF)
f4 = sm.Eq(xDD*nD + xDW*nW, xDF*nF)
f5 = sm.Eq(xAD*nD , .9*xAF*nF)
f6 = sm.Eq(xAW + xBW + xCW + xDW, 1.)
print(f1, f2, f3, f4, f5, f6)> Eq(0.95*nD + nW*xAW, 35.0)
> Eq(0.05*nD + nW*xBW, 40.0)
> Eq(nW*xCW, 20.0)
> Eq(nW*xDW, 5.0)
> Eq(0.95*nD, 4.5)
> Eq(xAW + xBW + xCW + xDW, 1)Jak je vidět, tímto způsobem jsme získali systém tzv. bilineárních
rovnic, který lineární řešitel linsolve nedokáže vyřešit.
Je tedy nutné provést vhodnou substituci bilineárních členů – v tomto
případě nahradíme molární zlomky ve zbytku rovnou látkovým množstvím
dané složky ve zbytku (xiW * nW = niW). Díky této
substituci dojde k přeformulování vazné podmínky na molární zlomky ve
zbytku a získáme celkovou látkovou bilanci zbytku. Dodefinujeme tedy
další symbolické proměnné a celou soustavu přepíšeme na tvar:
nAW, nBW, nCW, nDW = sm.symbols('nAW nBW nCW nDW')
ff1 = sm.Eq(xAD*nD + nAW, xAF*nF)
ff2 = sm.Eq(xBD*nD + nBW, xBF*nF)
ff3 = sm.Eq(xCD*nD + nCW, xCF*nF)
ff4 = sm.Eq(xDD*nD + nDW, xDF*nF)
ff5 = sm.Eq(xAD*nD , .9*xAF*nF)
ff6 = sm.Eq(nAW + nBW + nCW + nDW, nW)
print(ff1, ff2, ff3, ff4, ff5, ff6)> Eq(nAW + 0.95*nD, 35.0)
> Eq(nBW + 0.05*nD, 40.0)
> Eq(nCW, 20.0) Eq(nDW, 5.0)
> Eq(0.95*nD, 4.5)
> Eq(nAW + nBW + nCW + nDW, nW)Soustavu opět vyřešíme funkcí linsolve.
sol = sm.linsolve([ff1, ff2, ff3, ff4, ff5, ff6], (nD, nW, nAW, nBW, nCW, nDW))
print(sol)
nD, nW, nAW, nBW, nCW, nDW = sol.args[0]> {(33.1578947368421, 66.8421052631579, 3.49999999999999, 38.3421052631579, 20.0, 5.0)}Nyní zbývá pouze dopočítat molární zlomky v destilačním zbytku a zobrazit výsledky ve požadovaném formátu.
xAW, xBW, xCW, xDW = nAW/nW, nBW/nW, nCW/nW, nDW/nW
print(f"Destilát: {nD:.2f} kmol; Zbytek: {nW:.2f}")
print(f"Složení zbytku: {xAW*100:.1f} mol. % fenolu, {xBW*100:.1f} mol. % kresolu, {xCW*100:.1f} mol. % xylenolu, {xDW*100:.1f} mol. % těžších fenolů.")> Destilát: 33.16 kmol; Zbytek: 66.84 kmol.
> Složení zbytku: 5.2 mol. % fenolu, 57.4 mol. % kresolu, 29.9 mol. % xylenolu, 7.5 mol. % těžších fenolů.