6. Numerická integrace obyčejných diferenciálních rovnic (ODR)

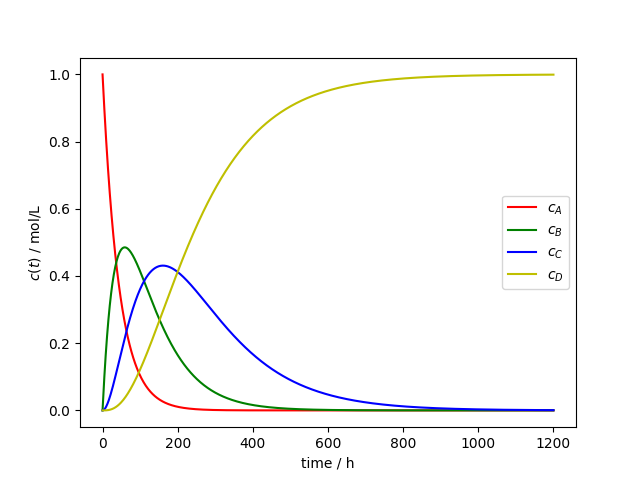
Pro ukázku numerické integrace ODR pomocí Pythonu využijeme příklad tří následných chemických reakcí ve vsádkovém reaktoru. Požíváme příklad z předmětu Modelování procesů v chemickém inženýrství. Schematicky lze tuto úlohu zaznačit jako

A → B → C → D,

pro každou reakci potřebujeme rychlostní konstantu k₁=0.02268 h⁻¹, k₂=0.01224 h⁻¹ a k₃=0.00702 h⁻¹.

Úlohu budeme řešit pomocí numerického řešiče soustav ODR odeint z balíčku scipy, proto je musíme nejprve naimportovat. Dále budeme potřebovat balíček numpy a pokud budeme chtít výsledek zobrazit v grafu, naimportujeme rovněž pyplot z balíčku matplotlib.

    import numpy as np
    from scipy.integrate import odeint
    from matplotlib import pyplot as plt

Nejprve si zadefinujeme konstanty k₁, k₂ a k₃.

    k1 = 0.02268 #h-1
    k2 = 0.01224 #h−1 
    k3 = 0.00702 #h-1

Soustavu diferenciálních rovnic zapíšeme jako funkci jejíž vstupními hodnotami bude list koncentrací c_i v čase t a tento čas. Tato funkce vrací vektor levých stran soustavy ODR tedy dc_i/dt.

    def ODEs(c,t):
        """
        Args:
            c (real,len=4): list of concerntrations of A,B,C,D in mol/L
            t (real): time in hours

        Returns:
            dcdt (real,len=4): list of concentration rates of A,B,C,D in mol/L/h
        """
        dcdt = np.zeros(4)
        dcdt[0] = -k1*c[0]
        dcdt[1] = k1*c[0] - k2*c[1]
        dcdt[2] = k2*c[1] - k3*c[2] 
        dcdt[3] = k3*c[2] 
        return dcdt

Před začátkem integrace musíme zvolit počáteční podmínku, tj. koncentrace v čase t = 0 h. My volíme c_A = 1 mol/L, a zbytek pro zbytek složek c_i = 0 mol/L. Následně musíme vytvořit vektor časů, ve kterých chceme vypsat výsledky soustavy ODR. K tomu poslouží funkce linspace z balíčku numpy. Násldně už můžeme zavolat řešič ODR odeint.

    c0 = [1,0,0,0]  #cA,cB,cC,cD in mol/L at t=0
    t = np.linspace(0, 1200, num=1000)
    c = odeint(ODEs, c0, t)

K zobrazení vysledků, průběhu koncentrací jednotlivých složek v čase použijeme pyplot z balíčku matplotlib.

    plt.plot(t, c[:,0], 'r', label='$c_A$')
    plt.plot(t, c[:,1], 'g', label='$c_B$')
    plt.plot(t, c[:,2], 'b', label='$c_C$')
    plt.plot(t, c[:,3], 'y', label='$c_D$')
    plt.xlabel('time / h')
    plt.ylabel('$c(t)$ / mol/L')
    plt.legend(loc='best')
    plt.show()

Takto získáme následující graf.