V této kapitole si ukážeme, jak proložit rovnovážná data z
předchozího oddílu pomocí (a) polynomu a (b) spline. Omezíme se pouze na
relativní zlomky acetonu v jednotlivých fázích, pro názornost si sloupce
z DataFrame data z předchozí demonstrace přejmenujeme na
x_data a y_data. Do rovnovážných dat přidáme
bod [0,0].
x_data = np.insert(data['Toluenová fáze.1'].values,0, 0.0)
y_data = np.insert(data['Vodná fáze.1'].values, 0,0.0)
print(type(x_data))> <class 'numpy.ndarray'>Připravíme si nový graf, který bude obsahovat data a výsledné interpolační křivky.
plt.figure()
plt.scatter(x_data, y_data, marker="o", label="Relativní zlomky")
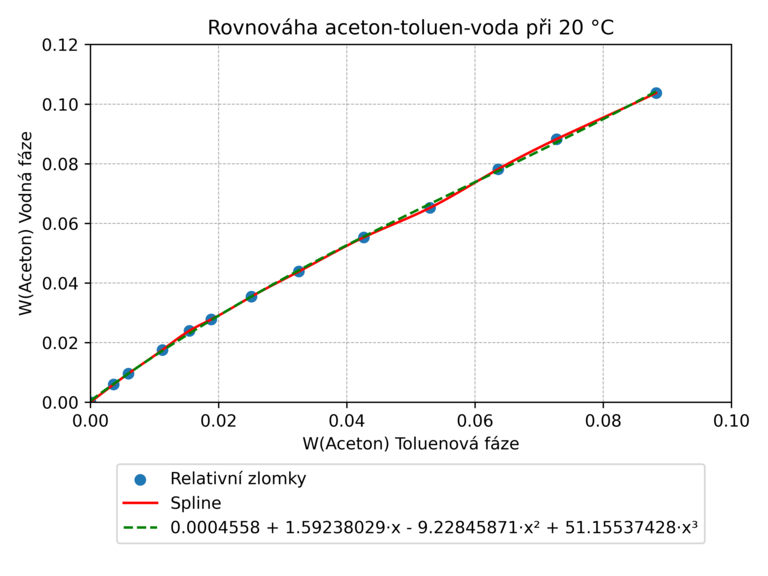
plt.title('Rovnováha aceton-toluen-voda při 20 °C')
plt.xlabel("W(Aceton) Toluenová fáze")
plt.ylabel("W(Aceton) Vodná fáze")
plt.xlim([0, 0.1])
plt.ylim([0, 0.12])
plt.grid(color='grey', linestyle='--', linewidth=0.5, alpha=0.7)Proložení polynomem je nejjednodušší způsob, jak aproximovat data.
Využijeme submodul numpy.polynomial z balíčku NumPy, který
obsahuje funkce pro práci s polynomy. Polynom stupně n je v tomto balíčku reprezentován
třídou Polynomial, která obsahuje metody pro výpočet hodnot
polynomu, derivací, integrálů a dalších operací. Proložení polynomem
stupně n daty ve smyslu
nejmenších čtverců provedeme následovně – vytvoříme instanci třidy
Polynomial pomocí metody Polynomial.fit.
Jakmile máme takto vytvořený polynom, můžeme vyčíslit funkční hodnotu v
bodě x tak, že k instanci
polynomu přistupujeme jako k funkci s argumentem x. Objekt polynomu můžeme také
zobrazit pomocí funkce print, seznam koeficientů polynomu
získáme pomocí atributu coef.
import numpy as np
from numpy.polynomial import Polynomial
p = Polynomial.fit(x_data, y_data, 3).convert()
x_poly = np.linspace(min(x_data), max(x_data), 100)
y_poly = p(x_poly)
print(p.coef)
print(p)> [ 7.64994420e-04 1.56862367e+00 -9.73046034e+00 5.71097709e+01]
> 0.00076499 + 1.56862367·x - 9.73046034·x² + 57.10977089·x³třída Polynomial je novinkou v NumPy v1.19.0, ve starších verzích se používala funkce
numpy.polyfit. Tato funkce je stále dostupná v dokumentaci její použití manuál v nových skriptech nedoporučuje.
Nyní zkusíme proložit naše rovnovážná data pomocí kubického spline.
Kubický spline je po částech definovaná kubická funkce, hledáme tedy 4
koeficienty polynomu 3. stupně pro každý z úseků mezi prokládanými body.
Po této interpolační funkci požadujeme, aby procházela všemi
prokládanými body (uzly). V uzlech dále požadujeme spojitost první a
druhé derivace. Aby byl kubický spline jednoznačně definován, je potřeba
klást dvě dodatečné podmínky (tzv. okrajové podmínky). Pro proložení
spline využijeme balíček SciPy, konkrétně třídu
CubicSpline z modulu scipy.interpolate.
Vytvoření instance CubicSpline je jednoduché, stačí zadat x
a y data jako první dva argumenty, následně můžeme danou instanci
CubicSpline použít jako funkci, která vrací hodnotu
interpolované funkce v zadaném bodě. Pokud explicitně nezadáme okrajové
podmínky, použije se výchozí tzv. “not-a-knot” okrajová podmínka, která
zjednodušeně řečeno říká, že jsou první dva okrajové polynomy stejné. O
tom, jaké okrajové podmínky lze zadat, se můžete dočíst v dokumentaci.
from scipy.interpolate import CubicSpline
f_spline = CubicSpline(x_data, y_data, bc_type='not a knot')
x_spline = np.linspace(min(x_data), max(x_data), 100)
y_spline = f_spline(x_spline)Nakonec zobrazíme výsledné proložení polynomem a spline na grafu.
plt.plot(x_spline, y_spline, label="Spline", color='red')
plt.plot(x_poly, y_poly, label=ßstr(p), color='green')
plt.legend(loc='upper left')
plt.show()
