Modelování 8: Lineární a nelineární regrese

V tomto článku bych chtěl ve stručnosti popsat, jakým způsobem lze v Matlabu provádět fitování dat, tj. proložit data přímkou, polynomem nebo jinou funkcí. Obecněji řečeno, jedná se optimalizační úlohu, kdy ze znalosti určitých (např. experimentálních) dat hledáme neznámé hodnoty parametrů, které určují konkrétní funkci tak, aby hodnoty získané touto funkcí (model) co nejlépe odpovídaly původním datům (experiment).

Ukážeme si to na příkladu adsorpční izotermy popsané vztahem

: $\displaystyle q = q_\mathrm{max}\frac{K p}{1+K p}$

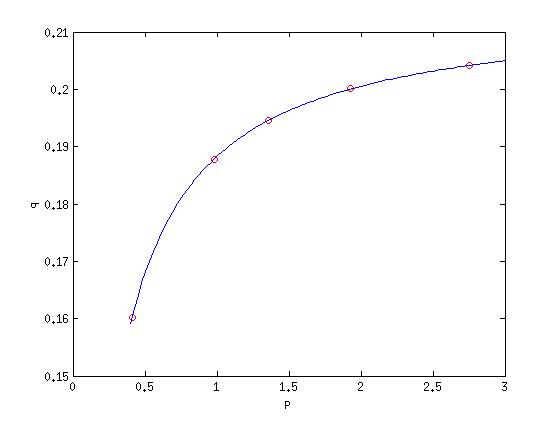
Máme tato data: závislost adsorbovaného množství na tlaku

p / MPa	0,41	0,98	1,36	1,93	2,75
q / g/g	0,1602	0,1878	0,1946	0,2001	0,2041

a chceme z nich vyhodnotit konstanty Langmuirovy rovnice: K a q_max.

Lineární regrese

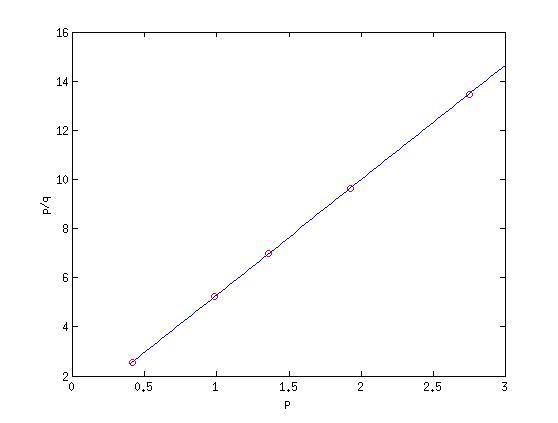
Lineární regresí myslíme nejenom proložení dat přímkou, ale i polynomem vyššího řádu nebo jinou lineární kombinací funkcí. Výše uvedenou adsorpční rovnováhu lze upravit (a tím linearizovat) do tvaru

: $\displaystyle\frac{p}{q}=\frac{1}{q_\mathrm{max}}p+\frac{1}{K q_\mathrm{max}}$

což je rovnice přímky y=a₁x+a₀, ve které platí

: $\begin{aligned}\displaystyle y&\equiv\frac{p}{q}\\ x&\equiv p\\ a_1&\equiv\frac{1}{q_\mathrm{max}}\\ a_0&\equiv\frac{1}{K q_\mathrm{max}}\end{aligned}$

Hledání koeficientů a₁ a a₀ metodou nejmenenších čtverců lze popsat jako hledání řešení přeurčené soustavy rovnic

: $\begin{aligned}\displaystyle y_1 &= a_1 x_1 + a_0\\ y_2 &= a_1 x_2 + a_0\\ &\cdots\\ y_N &= a_1 x_N + a_0 \end{aligned}$

kterou lze maticově zapsat ve tvaru

: $\displaystyle\begin{bmatrix} y_1\\ y_2\\ \cdots \\ y_N\end{bmatrix} = \begin{bmatrix} x_1 & 1 \\ x_2 & 1 \\ \cdots \\ x_N & 1\end{bmatrix} \begin{bmatrix} a_1 \\ a_0 \end{bmatrix}$

Řešením této soustavy lineárních rovnic je vektor koeficientů a, který lze určit například pomocí rovnice

: $\displaystyle \mathbf{y}=\mathbf{V}\,\mathbf{a} \rightarrow \mathbf{a} = (\mathbf{V}^\mathrm{T}\mathbf{V})^{-1}\mathbf{V}^\mathrm{T}\mathbf{y}$

Po matematickém úvodu si ukažme postup těchto operací v programu Matlab:

>> p = [0.41 0.98 1.36 1.93 2.75]; >> q = [0.1602 0.1878 0.1946 0.2001 0.2041]; >> x = p'; >> y = (p./q)';

Všimněte si, že vektory x a y jsme udělali sloupcové. Nyní sestavíme matici V. Sloupec jedniček lze pohodlně získat umocněním prvků ve vektoru x na nultou.

>> V = [x, x.^0] V = 0.41000 1.00000 0.98000 1.00000 1.36000 1.00000 1.93000 1.00000 2.75000 1.00000

Výše uvedenou přeurčenou soustavu je vhodné v Matlabu řešit pomocí operátoru \ (backslash). Tento operátor v našem případě hledá řešení pomocí QR faktorizace, což je výpočetně jednodušší než cesta přes dvakrát opakované násobení matic spojené s vyčíslením inverzní matice.

>> a = V \ y a = 4.66379 0.64667

Vidíme, že analogicky bychom mohli postupovat při lineární regresi pomocí lineární kombinace libovolných funkcí. Nicméně, pokud prokládáme data polynomem, lze stejnou práci vykonat rychleji použitím funkce polyfit a nemusíme se starat o konstrukci matice V.

>> a = polyfit(x,y,1) a = 4.66379 0.64667

Nakonec bude vhodné vizuálně prověřit, že nalezené koeficienty vedou k dobrému proložení dat a dopočítat hodnoty parametrů K a q_max

>> xx = linspace(0.4, 3, 100); >> yy = a(1)*xx + a(2); >> plot(x,y,'ro',xx,yy,'b-') >> qmax = 1/a(1) qmax = 0.21442

>> K = 1/(qmax*a(2)) K = 7.2120

Graf lineární regrese — Proložení dat adsorpční rovnováhy v linearizované formě

Nelineární regrese

Pokud budeme hledat hodnoty K a q_max přímo a použijeme adsorpční rovnováhu ve tvaru před její linearizací

: $\displaystyle q = q_\mathrm{max}\frac{K p}{1+K p}$

bude se jednat o nelineární regresi. Pro zjednodušení zápisu označíme hledané parametry q_max a K jako λ₁ a λ₂

: $\displaystyle q = \lambda_1\frac{\lambda_2 p}{1+\lambda_2 p}$

Hledání parametrů λ₁ a λ₂ je optimalizační úloha, kdy hledáme minimum funkce F(λ), kde λ=[λ₁,λ₂]. Tato funkce představuje součet čtverců odchylek

: $\displaystyle F([\lambda_1,\lambda_2]) = \sum_{i=1}^N \left(q_i - \lambda_1\frac{\lambda_2 p_i}{1+\lambda_2 p_i}\right)^2$

V Matlabu můžeme také využít funkci norm, která počítá Euklidovskou normu vektoru

: $\displaystyle |\mathbf{x}|=\sqrt{\sum_{i=1}^N x_i^2}$

Funkce, pro kterou budeme hledat minimum, bude vypadat takto

: $\displaystyle F([\lambda_1,\lambda_2]) = \sqrt{\sum_{i=1}^N \left(q_i - \lambda_1\frac{\lambda_2 p_i}{1+\lambda_2 p_i}\right)^2}$

Nyní si ukážeme postup v Matlabu. Zadáme data, která chceme proložit:

>> p = [0.41 0.98 1.36 1.93 2.75]; >> q = [0.1602 0.1878 0.1946 0.2001 0.2041];

Funkci definujeme v Matlabu pomocí tzv. anonymní funkce, odkaz na tuto funkci uložíme do proměnné F.

>> F = @(lam) norm(q-lam(1)*lam(2)*p./(1+lam(2)*p));

Potom je nutné zvolit počáteční odhad hodnot parametrů a nalézt hodnoty parametrů v minimu F pomocí fminsearch

>> lam0 = [0.1 0.1]; >> lam = fminsearch(F,lam0) lam = 0.21444 7.20278

A máme přímo hodnoty parametrů adsorpční rovnováhy. Nepatrné rozdíly v porovnání s regresí linearizovaného tvaru nás nemusí trápit. Nakonec se opět přesvědčíme, jestli nalezené parametry prokládají experimentální data dobře

>> pp = linspace(0.4, 3, 100); >> qq = lam(1)*lam(2)*pp./(1+lam(2)*pp); >> plot(p,q,'ro',pp,qq,'b-')

V našem jednoduchém případě vede lineární i nelineární regrese ke stejným výsledkům. Na závěr můžeme poznamenat, že výhodou nelineární regrese je její obecnost (tj. nejsme omezeni na linearizovatelné problémy a parametry získáme přímo). Naopak nevýhodou nelineární regrese je skutečnost, že se nedá zaručit, aby algoritmus za všech okolností našel globální minimum funkce. Výsledek nelineární regrese tak může být ovlivněn volbou počátečního odhadu.

Modelování 8: Lineární a nelineární regrese

Lineární regrese

Nelineární regrese

Published by

Zdenek Grof

Leave a Reply Cancel reply