Simulujte metodou MC tekutinu tuhých koulí v periodických okrajových podmínkách; průměr koulí nechť je 1. Zvolte zlomek stěsnání (packing fraction) y=(objem koulí)/(objem prostoru)=0.4. Měřte radiální distribuční funkci a stanovte g(1+) (limita zprava v kontaktu). Stanovte kompresibilitní faktor podle vzorce
z = P V / R T = 1 + 4 y g(1+)
Simulujte MD metodou LJ tekutinu v periodických okrajových podmínkách. Zvolte redukovanou teplotu T*=1.2 a hustotu rho*=0.8. Změřte viriálový tlak.
Simulujte MC nebo MD metodou soustavu N atomů interagujících potenciálem exp-6
s alpha = 12, epsilon=rm=1, uzavřených v kulovité nádobě s odpudivými stěnami danými potenciálem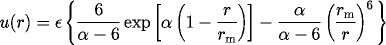
kde r je vzdálenost atomu od středu nádoby. Počáteční hustotu volte asi 0.5. Pomalu snižujte teplotu k nule. Co vznikne?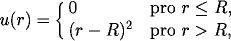
Napište program pro MC simulaci Isingova feromagnetu na kubické mřížce v periodických okrajových podmínkách. Monitorujte energii a celkovou magnetizaci (=součet všech spinů). Proveďte termální cyklus: pomalý ohřev z nízké teploty na vysokou a zpátky. Všimněte si hystereze. Podaří se vám odhadnout teplotu a druh fázového přechodu?
je soustava jednotkových vektorů ni na čtvercové mřížce s Hamiltoniánem
kde suma je přes nejbližší sousedy a
theta_i je úhel, který svírá
vektor ni s osou x. Simulujte metodou MC.
Moniturujte potenciální energii a celkovou magnetizaci (=součet všech
vektorů). Proveďte termální cyklus: pomalý ohřev z nízké teploty na
vysokou a zpátky. Podaří se vám odhadnout teplotu a druh fázového
přechodu?
Simulujte metodou MD systém N hmotných bodů interagujících Newtonovým gravitačním potenciálem. Jako počáteční podmínky volte 3D Gaussovo rozložení vzdáleností i rychlostí, "teplotu" určete z viriálového teorému (2K=-U). Podaří se vám dostat stabilní hvězdokupu?
Poznámka: je nutno vyřešit problém blízkých přiblížení. Lze použít Rungeovu-Kuttovu integrační metodu s proměnnou délkou kroku (např. že hvězda s nejvyšší rychlostí urazí během jednoho kroku max. jednu desetinu nejmenší vzdálenosti mezi hvězdami), případně trik popsaný v ukázce.
Uvažujte řetízek N atomů. Sousední atomy interagují potenciálem
U(ri,ri+1) = 100 [|ri-ri+1|2 - 1]2
a všechny nesousední atomy Lennardovým-Jonesovým potenciálem s epsilon = sigma = 1. Simulujte MD metodou. Monitorujte vzdálenost konců řetězce a gyrační poloměr rg daný vzorcem
Simulujte MC metodou zvanou "reptation" řetízek N atomů s pevnými délkami vazeb. Mezi atomy není (kromě pevných vazeb) žádná interakce. Koncové body jsou však natahovány stejně velkými opačně orientovanými silami ve směru osy x. Stanovte závislost "výchylky pružiny" <x1 - xN> na síle.
N souborů o různých délkách se má uložit na co nejmenší počet disket co nejvýhodnějším způsobem.
- Navrhněte vhodnou hodnotící funkci ("interakční energii") U.
- Navrhněte MC metodu; jeden zkušební krok může být přesun souboru z diskety na disketu.
- Simulujte za snižující se "teploty".
Nechť je dána mapa obsahující N měst. Některá města jsou spojena silnicí o známé délce. Pro každá dvě města existuje alespoň jedna cesta po silnici, která je spojuje; těchto cest může být více, přičemž (v této verzi problému obchodního cestujícího) není předem známo, která je nejkratší. Najděte co nejkratší uzavřenou cestu procházející alespoň jednou každým městem.
- "Konfigurace" je tedy posloupnost N nebo více měst, "energie" je délka trasy.
- Abychom se vyhnuli zachovávání podmínky, že dva sousedící členy posloupnosti musí být spojeny silnicí, můžeme říci, že nejsou-li dvě města spojena, je jejich vzdálenost rovna součtu všech vzdáleností na mapě.
- Zkušební kroky MC simulace musí dovolit i změnu počtu měst na trase (některými městy projdeme vícekrát).
- Jako počáteční "konfiguraci" zvolte N-tici (1, 2, ..., N).
- Simulujte za snižující se "teploty".
Uvažujte periodické okrajové podmínky založené na sc, fcc a bcc kubických mřížkách. Odvoďte tvary simulačních buněk, vzorce pro výpočet nejbližších sousedů a normalizaci polohy do základní buňky. Je-li kritériem efektivity maximální hodnota výrazu (vzdálenost středů buněk)/(objem)1/3, které okrajové podmínky jsou nejlepší?
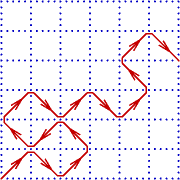Uvažujme tzv. dynamickou náhodnou procházku bez
protínání (dynamic self-avoiding walk) na
úhlopříčkách čtvercové mřížky Lx L, kde L je sudé.
"Chodec" začne procházku v bodě (0,0) ve směru (1,1).
V každém vrcholu s pravděpodobností 1/2 zatočí doleva a
s pravděpodobností 1/2 doprava s těmito výjimkami:
- Nikdy nejde podruhé stejnou cestou.
- Dole (y=0) a vlevo (x=0) se vždy "odrazí" (záporné souřadnice jsou zakázané).
- Nahoře (y=L) a vpravo (x=L) skončí.
Naprogramujte tuto náhodnou procházku a použijte:
- Generátor s posuvným registrem, např. R(103,250).
- Libovolný kongruenční generátor.
Zjistěte pravděpodobnost, že "chodec" skončí nahoře (y=L) a pokuste se vysvětlit případné odchylky.
Literatura: M. Ziff: Computers in Physics 12, 385 (1998)
Spočtěte závislost koeficientu difúze na koncentraci částic pro neinteragující mřížkový plyn na čtvercové dvoudimezionální mřížce. Srovnejte čas potřebný pro získání výsledku pro různé koncentrace. Možné rozšíření: pro mřížkový plyn s interakcí do nejbližších sousedů a pravděpodobností přeskoku částice danou Arrheniovým vztahem spočtěte závislost difúzní konstanty na teplotě.
Pomocí kinetického MC spočtěte časový vývoj pokrytí theta povrchu pevné látky pro různé pravděpodobnosti adsorpce piads a desorpce pides. Použijte modelu neinteragujícího dvoudimenzionálního mřížkového plynu s proměnným počtem částic. Výsledek srovnejte s analytickým řešením.
Uvažujte následující model šíření epidemií na čtvercové mřížce. V počátečním konfiguraci nechť je centrální vrchol ve stavu "N" (nakažený) a všechny ostatní ve stavu "Z" (zdravý). Aktivními vrcholy budeme rozumět nejbližší sousedy vrcholů ve stavu "N", kteří sami jsou ve stavu "Z". Aplikujte dále následující algoritmus:
- Vyber náhodně aktivní uzel.
- S pravděpodobností pi jej převeď do stavu "N", jinak jej převeď do stavu "I" (imunní).
Odhadněte kritickou hodnotu pravděpodobnosti onemocnění
pic pro to, aby nákaza zachvátila celý system.
Jak se změní situace jestliže do systému zavedeme pohyb?
Uvažujte k tomu účelu např. následující
mechanismus: vyber náhodně dvojici vrcholů a vyměň jejich stavy.
Napište program pro výpočet vlastních energií kvantového harmonického oscilátoru metodou dráhového integrálu. Určete přesnost metody v závislosti na velikosti "řetízkového polymeru" m.