Další úlohy
Úlohy označené * jsou již zahrnuty ve skriptech z r. 2003.
Molekulární dynamika
*
Vibrační spektrum molekul
| ion | at. hm.
[g/mol] | -Emin
[kcal/mol] | Rmin
[Angstrom] |
| Na+ | 22.9898 | 1.607143 | 1.0649016 |
| Cl- | 35.4530 | 0.1177885 | 2.4790916 |
Simulujte metodou MD klastr čtyř aniontů Cl- a čtyř
kationtů Na+. Ionty interagují, kromě elektrostatických
sil, Lennard-Jonesovým potenciálem s parametry danými v tabulce
(1 kcal=4.184 kJ, 1 A=10-10 m).
Parametry Emin a Rmin pro pár Na+--Cl- jsou
geometrickým průměrem parametrů obou složek.
Vyjděte z náhodné počáteční konfigurace s průměrnou vzdáleností iontů
asi 3 až 5 A (pozor na překryvy atomů!) Nejprve nalezněte
přibližné lokální mimimum simulací za snižující se teploty (použijte
metodu přeškálování rychlostí, případně frikční termostat) asi do
0.1 K. Vhodný integrační krok je asi 2 fs. Pak nastavte
náhodně rychlosti odpovídající zhruba 1 K a simulujte bez
termostatu (v mikrokanonickém souboru) aspoň několik desítek ps.
Měřte po asi 0.01 ps kinetickou energii, případně souřadnice
vybraných atomů, dipólmoment apod. a proveďte Fourierovu transformaci.
Zobrazte výsledné spektrum a pokuste se přiřadit frekvence normálních
vibračních módů, vyšší harmonické a kombinační frekvence.
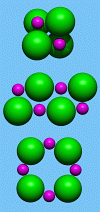
Poznámka: jsou (alespoň) tři lokální minima (čísla v závorkách jsou
tři nejnižší frekvence v jednotkách cm-1 stanovené metodou
diagonalizace matice druhých derivací potenciálu):
- krychle s ionty rozmístěnými stejně jako v základní buňce
krystalu NaCl (138.514, 139.069, 237.569)
- "pásek" 2x4 s šachovnicovitě rozloženými ionty (17.975,
47.379, 96.634)
- kruh (osmiúhelník) se střídavě rozloženými ionty (26.462,
31.439, 34.348)
Lagrangeovy body
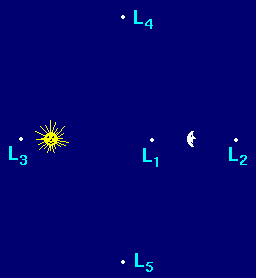
Lagrangeovy librační body v soustavě Slunce-planeta jsou body, v nichž
se malé těleso pohybuje synchronně s obíháním planety. Stabilní body
L4 a L5 leží ve vrcholech rovnostranného
trojúhelníka se základnou Slunce-planeta.
Napište program pro integraci pohybových rovnic tří těles. Počáteční
podmínky zvolte tak, aby planeta obíhala okolo Slunce po kruhové
dráze. Těleso o nepatrné hmotnosti umístěte do těsné blízkosti
L4 nebo L5 tak, aby obíhalo (téměř) synchronně.
Kontrolujte, zda jsou integrály pohybu konstantní. Zkuste vyjít
z bodů L1, L2, L3 nebo z náhodného
bodu.
*Tuhé koule
Napište program pro molekulární dynamiku tuhých pružných koulí
v periodických okrajových podmínkách. Možný algoritmus je následující:
- Vyjděte z jednoduché kubické mřížky o rozměru 53 nebo
63. Mřížkovou konstantu nastavte tak, aby zlomek stěsnání
(packing fraction) y=(objem koulí)/(objem prostoru)=0.4.
Koulím přiřaďte náhodné počáteční rychlosti
(na rozložení nezáleží - systém si vyrobí chaos sám).
- Pro všechny páry najděte čas, kdy dojde ke kolizi (pokud k ní
dojde). Pro dostatečně husté systémy stačí uvažovat nejbližší sousedy
v periodických okrajových podmínkách. Časy kolizí uschovejte v tabulce.
- Najděte čas první následující kolize a vypočtěte nové rychlosti
koulí po odrazu.
- Přepočtěte tabulku časů kolizí a pokračujte bodem 3.
Po zrovnovážnění stanovte kompresibilitní faktor podle vzorce
z = P V / R T = 1 + CR sqrt[(PI/3) (N/Ekin)]
kde CR = collision rate = počet kolizí za jednotku času.
Chladniho obrazce
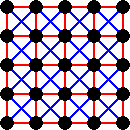Chladniho obrazce
vznikají při chvění desky posypané jemným práškem. Prášek se
shromáždí v uzlech.
Uvažujte diskrétní model čtvercové desky složený z NxN "atomů" v rovině; vhodné N je liché.
Nejbližší sousedé nechť interagují potenciálem U=r2-1,
Druzí nejbližší sousedé pak U=r2-2.
(V případě trojrozměrného modelu, tedy i příčných kmitů, je nutno
přidat ještě potenciál držící atomy v rovině.)
Naprogramujte pohybové rovnice (např. Verletovu metodu). Odlaďte - je
energie konstantní? Přidejte malé tlumení (např. obdobným způsobem
jako při metodě přeškálování rychlostí). K vybranému vrcholu přičtěte
budící sílu tvaru const cos(t omega(t)), kde omega(t) je pomalu se
měnící funkcí času. Pozorujte kmity. Zkuste desku pevně podepřenou
uprostřed (prostřední "atom" má mnohem větší hmotnost než
ostatní).
Monte Carlo
*
Preferenční vzorkování - částice v gravitačním poli
Naprogramujte příklad ze str. 91-92 skript. Měřte <x> i
s chybou - chybu je nutno stanovit velmi přesně (viz kap 10.5).
Srovnejte výsledky získané s p=1/2 (Metropolisovo vzorkování) a
p=1/3 (preferenční vzorkování).
Kapalný krystal
Uvažujte tuhé tyčinkové molekuly složené z asi 6-10 atomů vzdálených
1 (redukovaných jednotek). Atomy v různých molekulách spolu
interagují potenciálem (někdy nazývaným WCA LJ):
u(r) = 4r-12 - 4r-6 + 1, r<21/6
u(r) = 0, r>21/6
Napište program pro Monte Carlo simulaci v periodických okrajových
podmínkách a izobarickém souboru. Zvolte velmi řídkou počáteční
konfiguraci s náhodnými orientacemi molekul. Počet molekul by měl být
alespoň 200. Simulujte za zvyšujícího se tlaku a redukované teploty
T=1. Konečný tlak musí být poměrně vysoký, protože model nemá
přitažlivé síly.
Monitorujte parametr orientačního uspořádání. Počítejte s tím, že
vytvoření uspořádané struktury může, podle efektivity kódu, trvat i
několik dní simulací na běžném PC. Jakou strukturu dostanete?
Ukázka (získaná metodou MD) obsahuje 343 molekul a zobrazena je jen
jedna periodická simulační buňka.
Něco mezi MD a kinetickým Monte Carlo
NEW Dopravní zácpa
Simulujte chování aut na silnici za hustého provozu. Předpokládejte,
že volné auto se pohybuje rovnoměrně zrychleně (např. 2
m/s2), dokud nedosáhne maximální rychlosti (např. 36 m/s).
Pokud řidič uvidí před sebou jiné auto, začne zpomalovat. Bezpečná
vzdálenost přitom závisí na rychlosti (např. dráha, kterou auto ujede
za 1 s). Zpomalení by mělo záviset i na vzdálenosti (při velmi malé
vzdálenosti řidič musí dupnout na brzdu). Celý model by měl obsahovat
i prvek náhody (mírně různá zpomalení či zrychlení, různá bezpečná
vzdálenost různých řidičů ap.).
Celou simulaci proveďte v periodických podmínkách (okruh) s tím,
že na začátku auta stojí.
Při vhodném nastavení parametrů dojde ke vzniku kolon. Místo zácpy se
pohybuje opačným směrem než auta.
Kinetické Monte Carlo
NEW Evoluce barevného vidění u amerických opic
Samci amerických opic nerozlišují červenou a zelenou barvu, dvě
třetiny samic ano. Toto je důsledkem existence tří alel (označme je
A,B,C) pro pigmenty s mírně posunutou spektrální citlivostí. Gen
sídlí na pohlavním chromozomu X, který mají samci jen jeden, a proto
nemohou červenou a zelenou rozlišit. U samic se sejdou alely dvě;
pokud jsou různé, vidí opice barvy, pokud stejné, jsou na tom jako
samci. V populaci je všech tří alel stejně – musí tedy existovat
mechanismus, který toto rovnoměrné zastoupení udržuje, protože v
případě zcela náhodné dědičnosti časem jedna či dvě alely vymizí.
Vidět barevně je určitá evoluční výhoda, lze snáze rozlišit různě
barevné ovoce. Např. ale barvovidící opice typu AB může mít se samcem A
barvoslepého potomka AA, mechanismus udržující rovnoměrné zastoupení
alel je tedy jemnější.
Simulujte tento problém na populaci (alespoň) 10000 opic (5000 samců a 5000
samic) s počátečním zastoupením alel 20:4990:4990. V jedné generaci
proveďte náhodné spáření samců se samicemi a narození jednoho
potomka. Aby počet opic nerostl, vyhubte vždy 5000 nejstarších opic tak,
aby jich zbylo 10000.
Tady je však nutno zavést mírnou selekci, např. tak, že barvoslepé
opice s určitou pravděpodobností (cca 1 %) zahynou hlady nebo nemohou
mít potomka.
*
Růst sněhové vločky
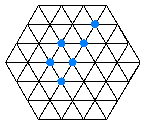
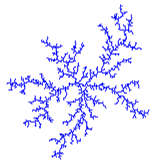Uvažujte hexagonální mřížku v rovině (každý vrchol má 6 rovnocenných
sousedů). Vrcholy buď jsou nebo nejsou obsazeny molekulou. Na
začátku simulace je jen jedna molekula uprostřed mřížky
šestiúhelníkového tvaru.
Jeden krok simulace popisuje difúzi molekuly z velké vzdálenosti až do
okamžiku, kdy se usadí na povrchu "vločky". Molekula se
objeví na náhodně vybraném vrcholu na obvodu mřížky. Potom molekula
náhodně difunduje - přeskakuje na libovolný sousedící vrchol (nemůže
však opustit mřížku) do té doby, kdy dosáhne vrcholu, který sousedí
s nějakým již obsazeným vrcholem. Tento krok se pak opakuje, až se
vytvoří dostatečně veliká vločka.
Algoritmus je možné modifikovat tak, že k depozici molekuly dojde jen
s určitou pravděpodobností. Tato pravděpodobnost může záviset na již
vytvořené vločce, např. tak, že je zvýhodněn růst směrem, v kterém již
leží několik molekul.
*
Požár pralesa
Uvažujte "les" na čtvercové mřížce v periodických
okrajových podmínkách. Každý vrchol mřížky se může nacházet ve
třech stavech: {živý strom, hořící strom, spáleniště}.
Nová konfigurace se generuje z předchozí podle pravidel:
- Má-li živý strom alespoň jednoho hořícího souseda (ze 4 sousedů),
pak vzplane
- Hořící strom shoří (v následující konfiguraci se změní ve spáleniště)
- Na spáleništi vyroste nový strom s pravděpodobností p
Vyjděte z konfigurace náhodně rozmístěnými stromy a spáleništi
v poměru 1:1 a s několika hořícími stromy. Vhodné p je několik %.
Úlohy označené * jsou již zahrnuty ve skriptech z r. 2003.
[Zpět na Informace pro studenty, skripta]
[Skripta: úlohy k řešení]
[back to J. Kolafa homepage]