| Strana, řádek nebo rov. | Chybně | Správně | Závažnost
Datum |
| 16 (2.16) | Lambda3 ve jmenovateli prostředního vzorce | Lambda3N | 1.12.00 |
| 22 (2.42) vpravo | e2 | ZJZKe2 | |
| 27 vsuvka za (3.1) | potenciál tvaru (2.28) | potenciál tvaru (2.28) a (2.29) | 13.2.00 |
| 27 vsuvka za (3.1) | fij, rij | fji, rji (pokud používáme konvenci rij=rj-ri) | 1.9.02 |
| 29 (3.9) | vzorec není potřeba | vynechat | 1.9.02 |
| 29 3 zdola | h dvě tečky r/2 | h2 dvě tečky r/2 | 13.2.00 |
| 30 (3.16) | + O(h) | + O(h2) | 2.2.00 |
| 30 (3.17) za = | tečka nad ri(t) | ri(t) | |
| 31 za (3.11) | ... podle vzorce (3.11). | ... podle vzorce (3.11) s tím, že místo y(r(t),t) se použije předchozí spočtené y, tedy y(rp(t),t). | 24.4.01 |
| 35 bod 2. a dále | pro Verletovu metodu ... roste střední odchylka s odmocninou času | Pro spojité potenciály i síly je chyba v dlouhých časech stacionární náhodná veličina (neroste s časem); to je proto, že metoda je symplektická (zachovává fázový objem) a Verletovu integraci lze přepsat jako přesnou integraci porušeného Hamiltoniánu. Pro potenciály jako LJ, které jsou spojité s výjimkou singularity pro rij=0, se objeví jak drift (bod 1.), tak šum rostoucí s časem (2.), ale obvykle jsou velmi malé. Další zdroje chyb (zaokrouhlovací, nespojitost potenciálu např. způsobená cutoffem) se zpravidla projevují jako šum (2.). | !
10.7.00 |
| 36 Obr. 3.4 | Vývoj kinetické energie | Vývoj celkové energie | 18.8.00 |
| 36 Obr. 3.4 | Ekin (v popisu osy y) | Etot | 18.8.00 |
| 38 Alg. 4.1 | Chybí odvození vzorce pro směrodatnou odchylku | Vypočteme z
stdev(X) = <(X-<X>)2/(n-1)>,
kde X=1 s pravděpodobností pi/4=nu/n
a X=0 s pravděpodobností 1-pi/4=1-nu/n | +
29.11.00 |
| 40-41 | | Jako příklad měřené veličiny (pozorovatelné) může sloužit:
- jestliže síť funguje, vydělám X(F)=2000Kč/den
- jestliže síť nefunguje, jen X(N)=500Kč/den.
Průměrný výdělek (střední hodnota) je
<X> = Sumi pii = pi(F)X(F) + pi(N)X(N) | +
29.11.00 |
| 47 Alg. 4.2 | chybí deklarace d | REAL d velikost zkušebního posunutí | |
| 47 Alg. 4.2 | aktualizace pole Epair je špatně | použít pomocné pole Ezkus[1..N], při výpočtu nové energie v něm uchovat všechny párové příspěvky Ezkus[j]:=u(r[j],rzkus) a v případě přijetí je dosadit do Epair v cyklu
FOR j:=1 TO N DO Epair[i,j]:=Epair[j,i]:=Ezkus[j]
správný algoritmus (PDF)
program v jazyce C | !!
15.10.99 |
| 57 (5.3) | prohozené r1 a rc | 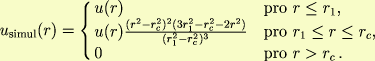 | 13.4.00 |
| 58 7-12 | jeden dipól ... | Energie jednoho dipólu v dutině v dielektriku je úměrná R-3, viz rov. (7.27). Popsaný problém "dielektrikum ovlivňuje dipolární systém, i když je nekonečně daleko" vznikne pro dipól(y) v periodických okrajových podmínkách (viz obr. 7.2). | !!
13.4.00 |
| 59 (5.5) | tečka ri | tečka xi (značí jednu kartézskou složku) | 13.4.00 |
| 62 Alg. 5.3 | Špatně znaménko: ff=(-du/dr/r) | ff=(+du/dr/r) (a z toho ff=-6/r8 atd.) | !
15.1.00 |
| 62 Alg. 5.3 | Ve smyčce dole: r[i] := r[i] + h*new[i] | r[i] := r[i] + h*new |
15.1.00 |
| 67 | | 1) Je užitečné si uvědomit smysluplnost definice g(r) (hlavně faktoru N(N-1)) následujícím vztahem pro energii na částici:
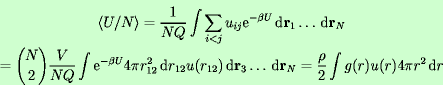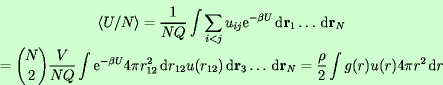
2) Občas se hodí vyjádření g(r) pomocí Diracovy delta-funkce:
g(r) = (1-1/N) V <delta r12-r> | +
29.11.00 |
| 69, (5.44) a (5.45) | krj, kr | k.rj, k.r (skalární součin) | 1.12.00 |
| 69 | Strukturní faktor je ve skriptech zaveden jako pomocná veličina vhodná k detekci krystalizace. |
Je to však především veličina, kterou lze
měřit pomocí neutronového, rentgenového či elektronového rozptylu a
z ní zpětnou Fourierovou transformací dostat radiální distribuční
funkci.
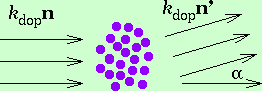 Nechť na vzorek dopadá vlna popsaná vlnovým vektorem
kdop = kdopn, kde
n je jednotkový vektor ve směru vlny. Amplituda vlny
rozptýlené o úhel alpha do směru n' je úměrná
Nechť na vzorek dopadá vlna popsaná vlnovým vektorem
kdop = kdopn, kde
n je jednotkový vektor ve směru vlny. Amplituda vlny
rozptýlené o úhel alpha do směru n' je úměrná
K = Sumj exp[i (kdopn - kdopn').rj] = Sumj exp[i k.rj] ,
kde jsme označili k = kdopn
- kdopn'. Protože k
= |k|
= 2 sin(alpha/2)kdop (a
kdop zůstává
v experimentu zpravidla konstantní), dostaneme na "stínítku"
(detektoru) v místě daném rozptylovým úhlem alpha signál úměrný
<|K|2>, což je úměrné S(k) podle
vzorce (5.44). Pro izotropní a homogenní tekutiny pak
S(k) = S(k) (viz 5.47).
Pokud napíšeme dr v (5.45) jako
r2 dr d cos(theta)
d phi, kde theta je úhel mezi vektory k a
r, a vyintegrujeme přes úhlové proměnné, dostaneme
k [S(k) - 1] = 4 pi rho Integral sin(kr) r [g(r)-1] d r .
Zpětná transformace je pak
rho r [g(r)-1] = 1/(2 pi2) Integral sin(kr) k [S(k) - 1] d k .
| +
1.12.00 |
| 70, obr. 5.5 | popis os: k | k2 | !
31.8.02 |
| 74, před 6.1.2 | | Takto jednoduchá je NPT simulace pouze pro atomární systémy. Pro tuhé molekuly s vazbami pevné délky je nutno škálovat jen pozice středu molekuly a neměnit relativní souřadnice atomů vzhledem ke středu. Pro větší částečně flexibilní molekuly i tato metoda selhává. | +
29.11.00 |
| 74 (6.8) | ...exp[betaP... | ...exp[-betaP... | 18.2.2002 |
| 79 12 zdola | Pro dvousložkový systém | vynechat | |
| 75 Alg. 6.1 | + beta*P*(Vzkus-V) | - beta*P*(Vzkus-V) | ! 18.2.2002 |
| 83 (6.38) | tau = 2 T eta | tau = (2 T eta)-1 | ! |
| 85 za (6.39) | (1/2)MVtečka V | (1/2)MVtečka V2 | 3.12.99 |
| 85 konec pozn. 8 | tečka xi | tečka xii | |
| 86 9 shora | kroucené P = P | Pcfg = P | 3.12.99 |
| 86 (6.45) | d/dt | d/dt' (i t má změněný fyzikální význam) | |
| 87 (6.47) | - U(r'N) | + U(r'N) | ! |
| 88 (6.54) a (6.57) | - U | + U | ! |
| 88 (6.56) | <A/s>/<1/s> | <A/s>'/<1/s>' | |
| 90 3 shora | tau < 1 | tau < 1 ps | |
| 95 (7.11) | opačně znaménka | beta Delta F = - ln<e-beta Delta U/2>prům + ln<e+beta Delta U/2>prům | ! |
| 97 (7.14) | chybí pravé závorky v čitateli a jmenovateli prvního zlomku | doplnit závorky | |
| 98, (7.21) | kj | k | 15.11.00 |
| 98, řádek 4 za (7.23) | (suma ve velké závorce) | M | |
| 100 (7.27) a (7.28) | M'j | M'i | |
| 100 pod (7.28) | kolem částice j | kolem částice i | |
| 105, řádek 3 | AB, BC, CA | AB, BC, CD | 21.3.02 |
| 105 nad (7.46) | při změně úhlu BCD | při změně dihedrálního úhlu
Vzorec (7.46) neplatí pro úhel BCD, platí však pro cos(BCD) - viz vsuvka na konci str. 103. V praxi je tato chyba malá, protože vazebné úhly fluktuují velmi blízko rovnovážné hodnoty. | !!
3.12.99 |
| 107, za (7.49) | snadno | po umocnění na druhou | +
29.11.00 |
| 107 (7.47) | r(t+h) | rSHAKE(t+h) - původní r(t+h) viz (3.13) | 7.5.99 |
| 107 (7.50), 108 (7.53) | chybí 2 ve jmenovateli | přidat faktor 2 do jmenovatele zlomku | !
7.5.99 |
| 109 (7.63) | calpha | cbeta | |
| 113 (8.4) vpravo | tečka p = - dH/dp | tečka p = - dH/dq | |
| 115, obr. 8.1 | křivka - - - | křivka odpovídá poněkud nižší hustotě; trojný bod argonu přitom je T=84K, rho=1410kg m-3 | 31.8.2002 |
| 113 (8.11) | K se nevykrátí | na pravé straně před <.> má být K beta | 5.12.01 |
| 116 (8.23) | tečka nad ri(0) | ri(0) | |
| 119 6 zdola | To je snadno vidět ... rozdílný, | vynechat | |
| 133 6 shora | |betaj> | |gammaj> | |
| 134 (9.26) | cosh pod odmocninou | sinh | 1.7.02 |
| 137 5 shora | pro M volit | pro m volit | |
| 143 (9.51) | psi* psi* | psi psi* | |
| 147 Poslední řádek Alg. 10.2 | ra | r | |
| 149 (10.6) | vzorec pro uGauss | 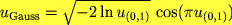 | !!
10.10.00 |
| 154 (10.20) | E=h4D | E=h4Det | 18.8.00 |
| 157 před (10.38) | rho | rho* | |
| 157 před (10.38) | (epsilon/NA)sigma3 | (epsilon/NA)sigma-3 | ! |
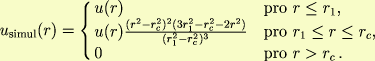
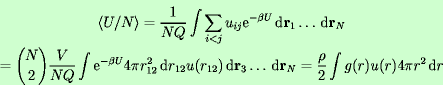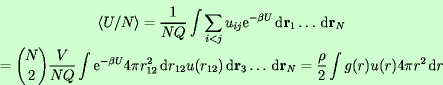
 Nechť na vzorek dopadá vlna popsaná vlnovým vektorem
kdop = kdopn, kde
n je jednotkový vektor ve směru vlny. Amplituda vlny
rozptýlené o úhel alpha do směru n' je úměrná
Nechť na vzorek dopadá vlna popsaná vlnovým vektorem
kdop = kdopn, kde
n je jednotkový vektor ve směru vlny. Amplituda vlny
rozptýlené o úhel alpha do směru n' je úměrná